www.eprace.edu.pl » obiektowe-bazy » Teoria » Algebra obiektowa

Algebra obiektowa

Algebra obiektowa jest z założenia matematyczną podstawą semantyki obiektowych języków zapytań, wzorującą się na algebrze relacji. W odróżnieniu od algebry relacyjnej, operatory wprowadzane przez algebrę obiektową działają na zbiorach obiektów i zwracają zbiory obiektów. Celem prac nad algebrami obiektowymi jest potrzeba takiego sformalizowania modelu obiektowego i semantyki języków zapytań, ażeby możliwe było przeprowadzanie dowodów poprawności technik optymalizacji zapytań.

Jak stwierdza autor [Subieta 1999a], cel ten nie został jak dotąd osiągnięty. Tenże autor uważa, iż obecnie istniejące propozycje algebr obiektowych są niespójne koncepcyjnie, dość skomplikowane, niedostatecznie uniwersalne i mają luźne związki z rygorystyczną matematyką.

Pomimo takowych opinii, istnieje wiele prób stworzenia algebry obiektowej. W niniejszej pracy oparto się na algebrze zaproponowanej w [Leung 1993]. Autorami tej algebry są dobrze znani na tym polu naukowcy. Jako że byli oni współtwórcami kilku wcześniejszych algebr, proponowana przez nich algebra AQUA jest efektem doświadczeń zdobytych podczas poprzednich prac.

Składnia

Wyrażenia w algebrze są reprezentowane przez termy. Term jest zmienną, stałą, symbolem funkcji (ang. function symbol), lambda abstrakcją (ang. lambda abstraction) formy

λ (x₁ : T₁, x₂ : T₂, ... , x_n : T_n) t : R,

lub aplikacji (ang. application)

t₀ (t₁ : T₁, ... , t_k : T_k) (t_k+1 : T_k+1, ... , t_n : T_n) : R,

gdzie t₀, t₁, ... , t_n są termami, a t₀ musi mieć typ funkcyjny (ang. function type).

Lambda abstrakcja może posiadać nazwę.

Przykładowo, niech nazwany term Names ma następującą postać:

Names = apply(λ(p)select_field(name)(p))(Persons),

term ten zwraca zbiór zawierający nazwiska każdej z osób ze zbioru Persons.

Apply (zdefiniowany w dalszej części pracy), select_field oraz name są symbolami funkcji, p jest zmienną, natomiast λ(p)select_field(name)(p) jest lambda abstrakcją.

Predykaty są funkcjami zwracającymi typ boolean. Są one tworzone z wykorzystaniem wbudowanych operatorów algebry AQUA i jej języka termów, opartego na rachunku lambda. Są one normalnie przekazywane jako parametry do operatorów takich jak: select, join, exists, czy foreall. Wszystkie zapytania w rezultacie tworzą nowy obiekt algebry.

Poniżej zaprezentowano oznaczenia wykorzystywane w dalszej części pracy do definiowania operatorów:

• A oraz B odnoszą się do wejściowych zbiorów lub wielozbiorów (ang. multisets).

• R jest wykorzystywane do oznaczenia wyjściowego zbioru lub wielozbioru, bądź też wynikowego zbioru lub wielozbioru.

• a służy do reprezentacji elementu wejściowego zbioru lub wielozbioru A.

• f, g oraz h służą do reprezentacji funkcji.

• id reprezentuje funkcję tożsamości (ang. identity function).

• p oznacza predykat.

• T oznacza typ wynikowy operatora.

• Krotki są oznaczane jako < >.

• L jest nazwą pola krotki.

• a/L oznacza wartość krotki a minus pole oznaczone L.

Inne oznaczenia będą definiowane w miarę potrzeb.

Typ parametrów

Parametryzowane konstruktory typu i wymagania związane z podtypami zaprojektowano tak, ażeby obsługiwały statyczną kontrolę typów. Rozwiązanie, które w tym celu przyjęto jest związane z wyraźnym podawaniem typu wynikowego jako parametru jednej z operacji algebry.

Wiele operacji opisywanej algebry tworzy instancje nowych typów jako wyniki. W związku z tym, wywnioskowanie typu wynikowego nie jest łatwym zadaniem, biorąc pod uwagę, że algebra zezwala na wielokrotne nadtypy i unie. Ażeby rozwiązać tę trudność i zapewnić elastyczność, algebra pobiera typ wynikowy jako parametr wejściowy operatorów, w których nie jest wymagany unikalny nadtyp przy występowaniu dwóch wejść o kompatybilnych (lecz nie identycznych) typach.

Równość

Niektóre typy mogą posiadać więcej niż jedną definicję pojęcia równości (ang. equality). Od każdego typu jest wymagane posiadanie domyślnej równości, która oznacza tożsamość. Wbudowane typy prymitywne (integer, float, boolean czy string) posiadają standardową definicję równości. W przypadku definiowania przez użytkownika nowego typu, musi zostać określona domyślna równość dla tego typu. Sensowne równości definiowane przez użytkownika powinny wywoływać relacje równości na wszystkich instancjach tego typu.

Równość jest niezbędna do zdefiniowania niektórych operatorów, jak na przykład unii.

Tożsamość stanowi domyślną równość dla elementów zbioru. Jeśli użytkownik chce narzucić na zbiór dodatkowe pojęcie równości, może je odpowiednio zdefiniować i dołączyć przykładowo do operatora dup_elim. Istotne jest, aby użytkownik w pierwszej kolejności wykonał operacje wymagające równości domyślnej. Warunek ten jest spowodowany tym, iż równość zdefiniowana przez użytkownika jest słabsza od równości domyślnej.

Operatory

W tym rozdziale przedstawione zostaną operatory algebry. Część z tych operatorów może zostać wyrażona poprzez użycie innych, co prowadzi do wielu redundancji w zbiorze operatorów. Zostały one jednak pozostawione częściowo dlatego, że pozwalają na tworzenie wyrażeń bardziej zwięzłych i przejrzystych, co byłoby niemożliwe po ich usunięciu, a częściowo dlatego, iż nadają się do specjalizowanych implementacji i optymalizacji, które są bardziej wydajne, niż gdyby zostały stworzone z wykorzystaniem operatorów bardziej ogólnych.

Operatory zbiorowe

Podrozdział ten przedstawia operatory zbiorowe (ang. set operators) omawianej algebry. Większość z tych operatorów wywodzi się z podobnych operatorów przedstawianych w literaturze. Autorzy algebry dokonali pewnych kombinacji, mających na celu uczynienie obecnego podejścia bardziej elastycznym w porównaniu z poprzednimi próbami.

Poniżej przedstawiona została lista wszystkich operatorów dla zbiorów, wraz z krótką definicją każdego z nich.

Pierwszą grupą operatorów są zbiorowe operatory jednoargumentowe (ang. unary set operators). Zostały one zdefiniowane następująco:

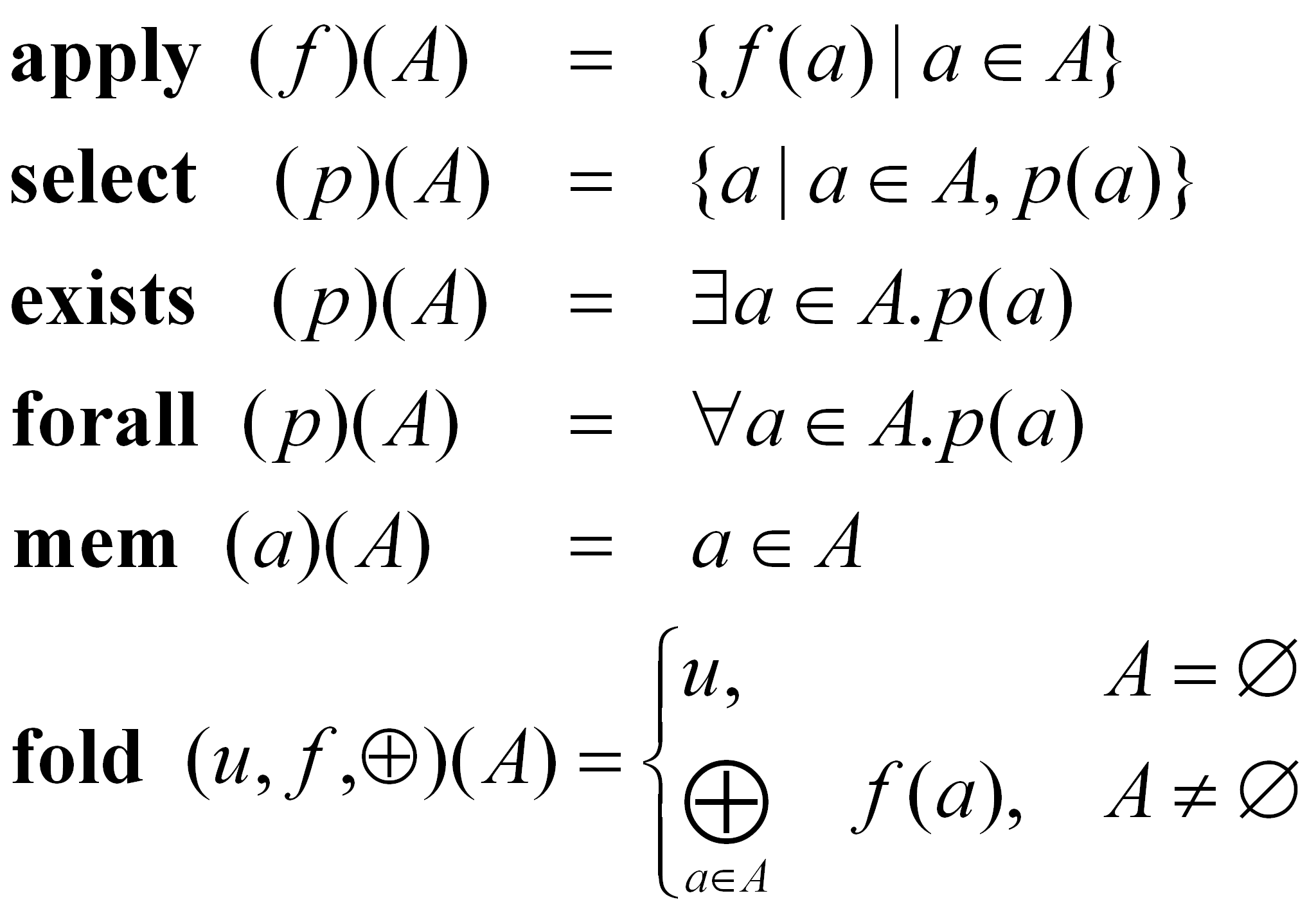
Operator fold jest mocnym operatorem. Wyrażenie fold(u,f,⊕)(A) redukuje zbiór A do pojedynczej wartości poprzez zastosowanie funkcji f do każdego jego elementu i iteracyjne łączenie otrzymanego wyniku z operatorem ⊕. Zastosowanie fold do pustego zbioru w efekcie daje u.

Operatory exists, forall oraz mem zwracają wartość typu boolean. Mogą być więc wykorzystywane jako rodzaj predykatów.

Kolejną grupę stanowią zbiorowe operatory dwuargumentowe (ang. binary set operators):

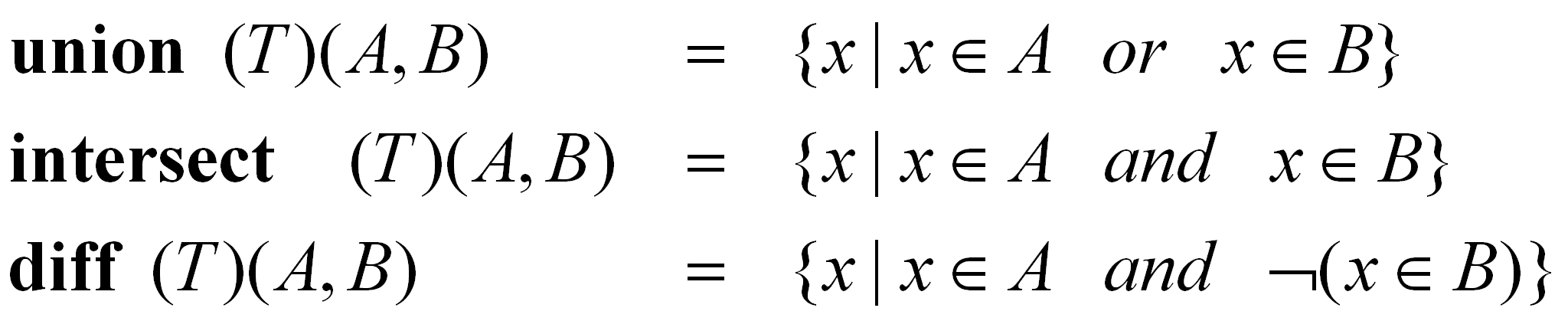
Operatory zbiorowe dwuargumentowe union, intersect oraz diff są operatorami znanymi z teorii zbiorów. Mimo tego przedstawione definicje są bardziej skomplikowane z uwagi na konieczność uwzględnienia typów. Podczas stosowania operatora dwuargumentowego nie jest wymagane, ażeby rozpatrywane zbiory były tego samego typu. Wystarczy, aby ich elementy miały przynajmniej jeden wspólny nadtyp, jako że domyślna równość tego nadtypu jest używana do porównań. Operatory te wykorzystują dodatkowy argument T, określający typ wynikowy. Typem wynikowym operatora union musi być nadtyp typów zbiorów wejściowych. W przypadku operatora intersect typ wynikowy może być zarówno nadtypem typów wejściowych, jak i jednym z tych typów. Ostatecznie, w przypadku operatora diff, typ wynikowy musi być albo typem pierwszego zbioru wejściowego, albo jego nadtypem.

Operatory określane mianem zbiorowych operatorów przekształcających (ang. set restructuring operators) to:

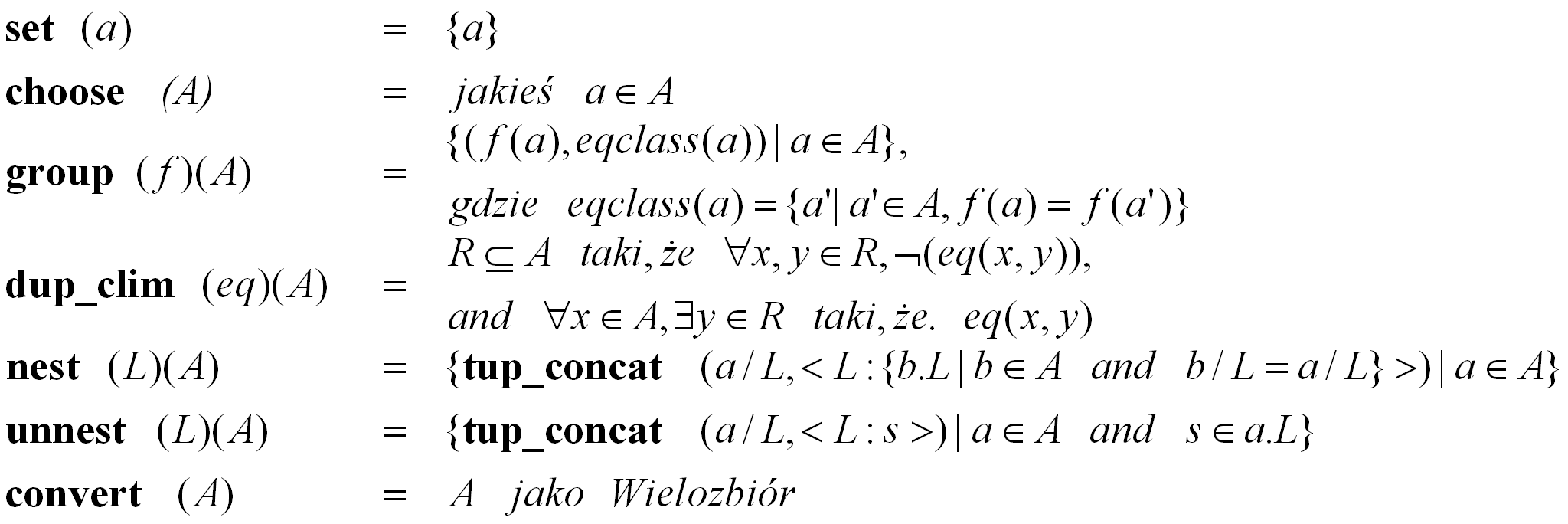
Na pewną uwagę zasługują tutaj dwa operatory, a mianowicie zagnieżdżania (nest) oraz rozgnieżdżania (unnest). Zostały one zdefiniowane jako wykorzystujące pojedyncze pole krotki L. Jednakże definicja ta może zostać w łatwy sposób rozszerzona do listy pól. W takim przypadku a/L odnosi się do wartości krotki a minus pola w liście L, natomiast a.L jest konkatenacją wartości wszystkich pól listy L.

Poniżej przedstawiono definicje operatorów złączenia (ang. join operators):

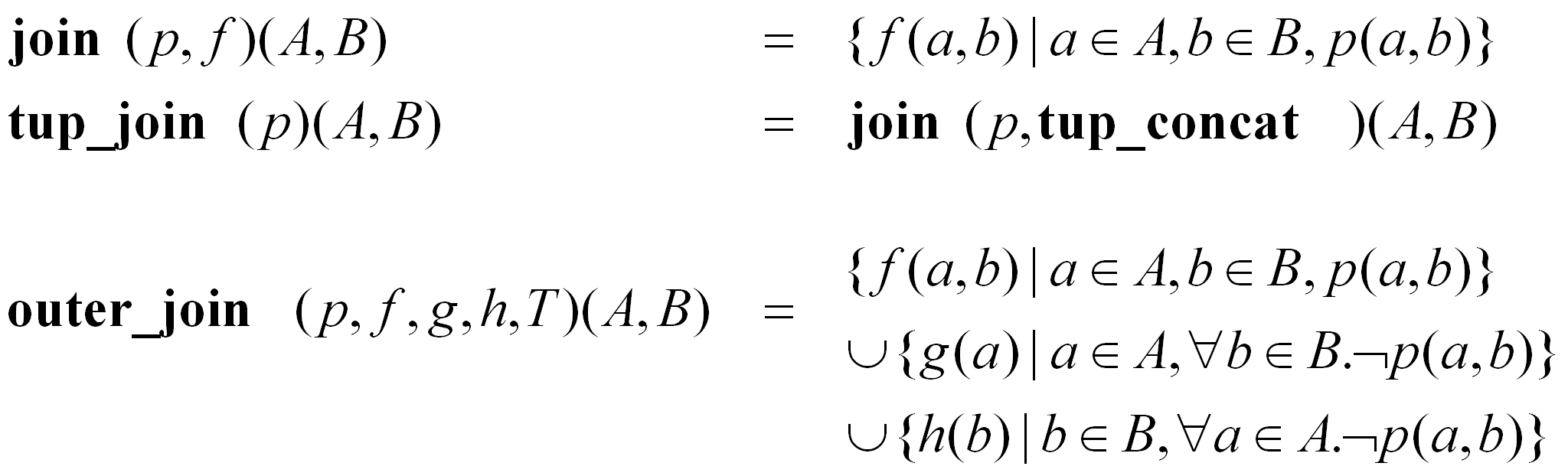
Operatory złączenia wymagają uwagi ze względu na ich ogólność. Operator join przyjmuje jako parametr funkcję, umożliwiając przez to użytkownikowi na definiowanie funkcji „łączącej”. Pozostałe operatory złączenia są podobnymi uogólnieniami wymagającymi predykatu i funkcji.

Typ wynikowy T operatora outer_join musi być nadtypem typów wynikowych funkcji f, g oraz h, ażeby umożliwić powiązanie rezultatów funkcji.

Znane operatory złączeniowe, takie jak: natural_join, equijoin, semijoin czy antijoin, nie zostały zdefiniowane jako prymitywy (ang. primitives) w omawianej algebrze, lecz w łatwy sposób mogą zostać wyrażone z wykorzystaniem zdefiniowanych operatorów.

Ostatnim przedstawianym operatorem zbiorowym jest operator najmniej stałego punktu (ang. least fixed point operator):

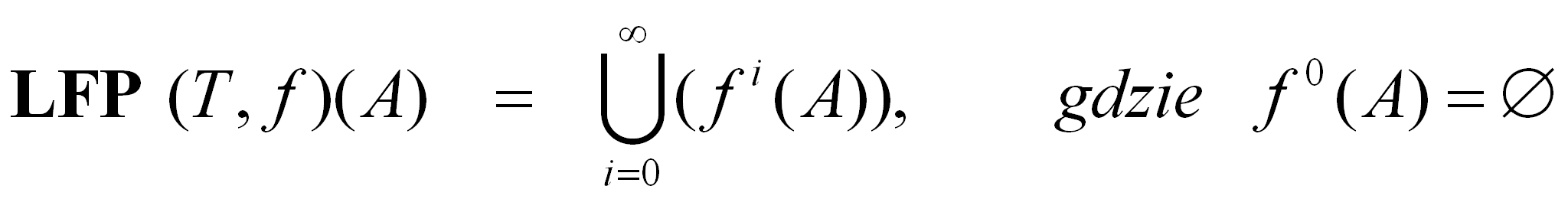
W przypadku tego operatora należy przyjąć następujące założenia w stosunku do funkcji f . Jest ona funkcją T→T, gdzie T jest typem zbioru A, a także musi być monotoniczna.

Poniżej zaprezentowano krótki przykład ilustrujący wykorzystanie operatorów. Rozważono zapytanie, które znajduje wszystkie osoby mieszkające w tym samym mieście w którym pracują, a następnie grupuje je w oparciu o nazwę tego miasta.

Przedstawione rozwiązanie wykorzystuje pole employer obiektu Person.

Wyrażenie A.B jest skrótem oznaczającym wywołanie metody B na obiekcie A.

Omówione zapytanie wygląda następująco:

LiveWhereWorkPeople =

select(λ(x)x.address = x.employer.address)(Persons)

Następnie należy zastosować operator group w celu pogrupowania osób z LiveWhereWorkPeople według ich miejsca zamieszkania.

Prezentuje to poniższy przykład:

group(λ(x)x.address)(LiveWhereWorkPeople)

W efekcie otrzymano zbiór uporządkowanych par postaci (city, people), gdzie city jest nazwą miasta w którym przynajmniej jedna osoba mieszka i pracuje, natomiast people jest zbiorem obiektów Person, reprezentujących wszystkie osoby mieszkające i pracujące w tym mieście.

Operatory wielozbiorowe

W przypadku wielozbiorów obsługiwane są praktycznie te same operacje, co w przypadku zbiorów, w większości przypadków z bardzo podobną semantyką.

Różnica pomiędzy wielozbiorami oraz zbiorami polega na tym, że wielozbiór może zawierać wielokrotne wystąpienia tego samego elementu. Notacją wykorzystywaną do oznaczenia wielozbiorów jest: {*e₁, e₂, ..., e_n*}, gdzie e_i oznacza elementy wielozbioru.

Zdefiniowano także pojęcie „krotności elementu” (ang. cardinality of an element) wielozbioru, jako liczbę wystąpień tego elementu w wielozbiorze. Zapis |A|_a oznacza „krotność elementu a w wielozbiorze A”. Można mówić także o „liczności wielozbioru” |A|, oznaczającej całkowitą ilość elementów, z uwzględnieniem wszystkich powtórzeń elementów.

Większość operatorów wielozbiorowych jest podobna do odpowiadających im operatorów zbiorowych, za wyjątkiem tego, że typami wejściowymi i wyjściowymi zamiast zbiorów są wielozbiory. Większość z przedstawionych dotychczas definicji jest prawdziwa także dla wielozbiorów.

Wyjątki stanowią zdefiniowane poniżej operatory:

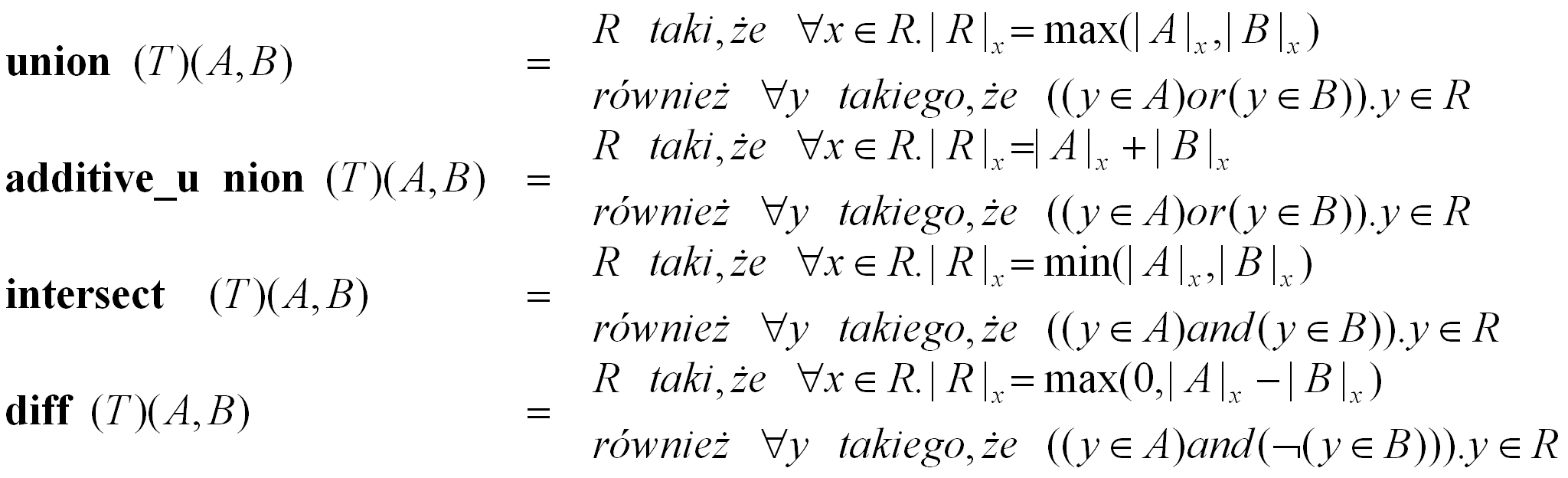
Operatory multiset oraz convert są to wielozbiorowe operatory przekształcające (ang. multiset restructuring operators). Natomiast operatory union, additive_union, intersect oraz diff to wielozbiorowe operatory dwuargumentowe (ang. binary multiset operators).

W przypadku wielozbiorowych operatorów dwuargumentowych występuje największe odstępstwo od odpowiadających im operatorów zbiorowych. Wszystkie te operatory w przypadku wielozbiorów bazują na pojęciu liczności elementów.

Operatory innych typów

Poza zbiorami i wielozbiorami, omawiana algebra obsługuje mnóstwo innych typów.

Unia jest typem, który wraz ze swym konstruktorem pozwala na tworzenie unii z dyskryminatorem (ang. discriminated union). Operacje zdefiniowane dla tego typu to: union, tagcase oraz typecase. Operacja union(U, tag, e) tworzy instancję unii U i inicjalizuje jej zawartość jako jednostkę e z etykietą tag. Zarówno tagcase(e), jak i typecase(e) selektywnie wykonują zbiór termów bazujący albo na etykiecie, albo na typie instancji unii e.

Typy funkcyjne reprezentują funkcje, które pobierają kilka typowanych parametrów i zwracają pojedynczą wartość typowaną. Nie istnieje wyraźny konstruktor typów funkcyjnych. Zamiast tego, instancje typów funkcyjnych są tworzone z wykorzystaniem typowanych wyrażeń lambda.

Typ boolean jest wykorzystywany do reprezentowania wartości prawdy i fałszu. Jest on wykorzystywany przy porównaniach i testowaniu wyrażeń warunkowych. Na typie boolean można wykonywać operacje and, or oraz not.

Ostatecznie, abstrakcyjne typy danych są to typy zbiorowe, których elementy są dostępne tylko poprzez użycie specjalnych funkcji, nazywanych interfejsem. Funkcje są dostępne poprzez operator invoke(I, f), który wywołuje funkcję f na instancji I.

komentarze

Przeszukaj ePrace

Copyright © 2008-2010 EPrace oraz autorzy prac.